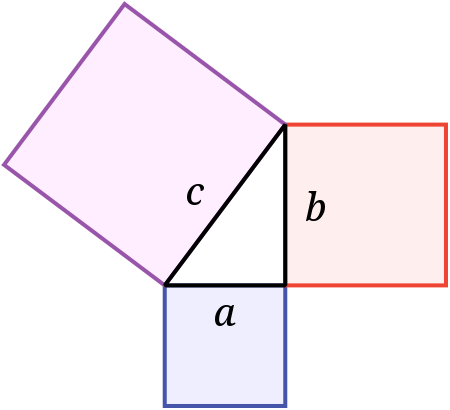
ในวิชาคณิตศาสตร์ ทฤษฎีบทพีทาโกรัส แสดงความสัมพันธ์ในเรขาคณิตแบบยุคลิด ระหว่างด้านทั้งสามของสามเหลี่ยมมุมฉาก กำลังสองของด้านตรงข้ามมุมฉากเท่ากับผลรวมของกำลังสองของอีกสองด้านที่เหลือ ในแง่ของพื้นที่ กล่าวไว้ดังนี้ ในสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านตรงข้ามมุมฉาก เท่ากับผลรวมพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านประชิดมุมฉากของสามเหลี่ยมมุมฉากนั้น ทฤษฎีบทดังกล่าวสามารถเขียนเป็นสมการสัมพันธ์กับความยาวของด้าน a, b และ c ได้ ซึ่งมักเรียกว่า สมการพีทาโกรัส ดังด้านล่าง[1]a2+b2=c2 (อาจแทนด้วยตัวแปรอื่นเช่น x, y, z, ก, ข, ค) โดยที่ c เป็นความยาวด้านตรงข้ามมุมฉาก และ a และ b เป็นความยาวของอีกสองด้านที่เหลือ ทฤษฎีบทพีทาโกรัสตั้งตามชื่อนักคณิตศาสตร์ชาวกรีก พีทาโกรัส ซึ่งถือว่าเป็นผู้ค้นพบทฤษฎีบทและการพิสูจน์[2][3] แม้จะมีการแย้งบ่อยครั้งว่า ทฤษฎีบทดังกล่าวมีมาก่อนหน้าเขาแล้ว มีหลักฐานว่านักคณิตศาสตร์ชาวบาบิโลนเข้าใจสมการดังกล่าว แม้ว่าจะมีหลักฐานหลงเหลืออยู่น้อยมากว่าพวกเขาปรับให้มันพอดีกับกรอบคณิตศาสตร์[4][5] ทฤษฎีบทดังกล่าวเกี่ยวข้องกับทั้งพื้นที่และความยาว ทฤษฎีบทดังกล่าวสามารถสรุปได้หลายวิธี รวมทั้งปริภูมิมิติที่สูงขึ้น ไปจนถึงปริภูมิที่มิใช่แบบยูคลิด ไปจนถึงวัตถุที่ไม่ใช่สามเหลี่ยมมุมฉาก และอันที่จริงแล้ว ไปจนถึงวัตถุที่ไม่ใช่สามเหลี่ยมเลยก็มี แต่เป็นทรงตัน n มิติ ทฤษฎีบทพีทาโกรัสดึงดูดความสนใจจากนักคณิตศาสตร์เป็นสัญลักษณ์ของความยากจะเข้าใจในคณิตศาสตร์ ความขลังหรือพลังปัญญา มีการอ้างถึงในวัฒนธรรมสมัยนิยมมากมายทั้งในวรรณกรรม ละคร ละครเพลง เพลง สแตมป์และการ์ตูน