ความน่าจะเป็น

การทดลองสุ่ม

การทดลองสุ่ม คือ การทดลองที่รู้ผลลัพธ์อาจจะเป็นอะไรได้บ้าง แต่ไม่รู้แน่นอนว่าแต่ละครั้งที่ทดลองจะได้ผลลัพธ์เป็นอย่างไร เช่น การทอยลูกเต๋าหนึ่งลูกหนึ่งครั้ง แต้มบนหน้าลูกเต๋าที่อาจจะเป็นได้คือ 1,2,3,4,5,6 แต่บอกไม่ได้แน่นอนว่าแต้มที่จะได้เป็นอะไร

ปริภูมิตัวอย่าง คือ เซตของผลลัพธ์ที่อาจจะเป็นไปได้ทั้งหมดของการทดลองสุ่ม นิยมเขียนแทนด้วย S

เหตุการณ์ คือ เซตของผลลัพธ์ที่เราสนใจจากการทดลองสุ่ม นิยมเขียนแทนด้วย E ดังนั้นจะสังเกตได้ว่า เหตุการณ์จะเป็นสับเซตของปริภูมิตัวอย่างเสมอ

ตัวอย่าง ในการโยนเหรียญ 2 ครั้ง ถ้าผลลัพธ์ที่สนใจ คือ หน้าของแต่ละเหรียญ จงหาปริภูมิตัวอย่าง และเหตุการณ์ที่เหรียญออกหัวอย่างน้อย 1 ครั้ง
วิธีทำ

• ให้ H แทนเหรียญออกหัว
• T แทนเหรียญออกก้อย
• E คือ เหตุการณ์ที่ออกหัวอย่างน้อย 1 ครั้ง

ดังนั้น

• S = {HH, HT, TH, TT}
• E = {HH, HT, TH}

ตัวอย่าง ในกล่องใบหนึ่งมีสลากหมายเลข 1 ถึง 9 อยู่หมายเลขละ 1 ใบ สุ่มหยิบสลากขึ้นมา 2 ใบ พร้อมๆกัน จงหาเหตุการณ์ที่ผลรวมของหมายเลขที่หยิบได้เป็น 9
วิธีทำ

• S = เหตุการณ์ทั้งหมดที่เป็นไปได้ในการหยิบสลาก 2 ใบขึ้นมาพร้อมกัน
• S = {(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8), (1,9), (2,3), (2,4), (2,5), (2,6), (2,7), (2,8), (2,9), (3,4), (3,5), (3,6), (3,7), (3,8), (3,9), (4,5), (4,6), (4,7), (4,8), (4,9), (5,6), (5,7), (5,8), (5,9), (6,7), (6,8), (6,9), (7,8), (7,9), (8,9)}
• E คือ เหตุการณ์ที่ผลลัพธ์รวมกันได้ 9

ดังนั้น

• E = {(1,8), (2,7), (3,6), (4,5)}

ความน่าจะเป็น

ต่อเนื่องจากการทดลองสุ่มและเหตุการณ์ ให้ S เป็นปริภูมิตัวอย่างที่เป็นเซตจำกัด และสมาชิกทุกตัวของ S มีโอกาสเกิดขึ้นเท่าๆกัน และ E เป็นเหตุการณ์ที่เป็นสับเซตของ S

ความน่าจะเป็นของเหตุการณ์ E เขียนแทนด้วย P(E) โดย

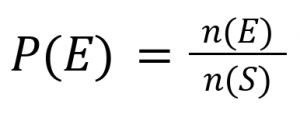
สมบัติของความน่าจะเป็น

1. 0 ≤ P(A) ≤ 1 หรือ ความน่าจะเป็นจะมีค่าระหว่าง 0 ถึง 1
2. P(S) = 1
3. P(∅) = 0
4. P(A∪B) = P(A) + P(B) – P(A∩B)
5. P(A’) = 1 – P(A)
6. P(A-B) = P(A) – P(A∩B)

ตัวอย่าง ในการโยนเหรียญ 2 ครั้ง จงหาความน่าจะเป็นของเหตุการณ์ที่เหรียญออกหัวอย่างน้อย 1 ครั้ง วิธีทำ

• ให้ H แทนเหรียญออกหัว
• T แทนเหรียญออกก้อย
• E คือ เหตุการณ์ที่ออกหัวอย่างน้อย 1 ครั้ง

ดังนั้น

• S = {HH, HT, TH, TT}
• E = {HH, HT, TH}
• P(E) = ^n(E)⁄_n(S) = ³⁄₄

ตัวอย่าง ในกล่องใบหนึ่งมีสลากหมายเลข 1 ถึง 9 อยู่หมายเลขละ 1 ใบ สุ่มหยิบสลากขึ้นมา 2 ใบ พร้อมๆกัน จงหาความน่าจะเป็นของเหตุการณ์ที่ผลรวมของหมายเลขที่หยิบได้เป็น 9 วิธีทำ

• S = เหตุการณ์ทั้งหมดที่เป็นไปได้ในการหยิบสลาก 2 ใบขึ้นมาพร้อมกัน
• S = {(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8), (1,9), (2,3), (2,4), (2,5), (2,6), (2,7), (2,8), (2,9), (3,4), (3,5), (3,6), (3,7), (3,8), (3,9), (4,5), (4,6), (4,7), (4,8), (4,9), (5,6), (5,7), (5,8), (5,9), (6,7), (6,8), (6,9), (7,8), (7,9), (8,9)}
• E คือ เหตุการณ์ที่ผลลัพธ์รวมกันได้ 9

ดังนั้น

• E = {(1,8), (2,7), (3,6), (4,5)}
• P(E) = ^n(E)⁄_n(S) = ⁴⁄₃₆